# all_flag
Esta implementación trata de reproducir el paper Prediction of Dengue Cases in Paraguay Using Artificial Neural
Networks simulando una situación donde el dataset está distribuido en diferentes entidades y por motivos de privacidad, los mismos no pueden ser compartidos entre entidades.
Motivación¶
Las tecnicas de machine learning pueden ayudar a mejorar el diagnostico de enfermedades, como detección de tumores en imagenes de MRI, detectar con tiempo retinopatía diabética en imagenes de retina, detección de cancer en imagenes de melanoma, hasta detectar el brotes de enfermedades entre varias otras aplicaciónes más. Pero este tipo de datos son bastante sensibles ya que son datos de los pacientes, una filtración de este tipo de información sería muy grave.
Pero no solo filtraciones, por culpa de varios escandalos respecto al uso de los datos sensibles de usuarios de parte de grandes empresas como Equifax, Facebook y Google generaron gran desconfianza en los mismos sobre como estos manipulan datos de sus usuarios. Un caso reciente es el uso de datos de pacientes para el Proyecto Nightingale de Google, el cual se encuentra bajo examinación por parte del gobierno estadounidense:
Mediante técnicas de preservación de privacidad como Federated Learning, Differential Privacy, Homomorphic Encryption entre otros es posible crear modelos útiles preservando la privacidad de los datos de los usuarios
Obs.: En el notebook de federated learning se dan más detalle sobre federated learning, homomorphic encryption y sus posibles aplicaciónes
import os
import sys
module_path = os.path.abspath(os.path.join('..'))
if module_path not in sys.path:
sys.path.append(module_path)
sys.setrecursionlimit(15000)
Los modelos de este notebook se desarrollaran utilizando el framework desarrollado en los notebooks anteriores.
Se importan las clases necesarias para definir una red neuronal del framework lightdlf además de definirse un método de evaluación del modelo
import numpy as np
import pandas as pd
import copy
import phe
from lightdlf_old.cpu.core import Tensor
from lightdlf_old.cpu.layers import Linear, Relu, Sigmoid, Tanh, MSELoss, Sequential
from lightdlf_old.cpu.optimizers import SGD
np.random.seed(123)
def rmse (pred, y):
se_sum = 0
for i in range(len(pred)):
se = (pred[i] - y[i]) * (pred[i] - y[i])
se_sum += se
mse = se_sum/len(pred)
rmse = np.sqrt(mse)
return rmse
Se carga el dataset con datos epidemiológicos y climatológicos
df = pd.read_csv('datasets/dengue/asu_dengue_dataset.csv')
df.head()
# for column in df.columns:
# print(column)
Se toman las columnas mencionadas en el paper para la creación del modelo
df_reduced = df[['cantidad',
'cantidad(-1)',
'temperatura_max_media(-1)',
'temperatura_max_media(-2)',
'temperatura_max_media(-3)',
'temperatura_max_media(-4)',
'temperatura_max_media(-5)',
'temperatura_max_media(-6)',
'temperatura_max_media(-7)',
'temperatura_max_media(-8)',
'temperatura_max_media(-9)',
'temperatura_max_media(-10)',
'temperatura_max_media(-11)',
'lluvia_mm(-1)',
'lluvia_mm(-2)',
'humedad_min_media_porc(-1)',
'humedad_min_media_porc(-2)',
'humedad_min_media_porc(-3)',
'humedad_min_media_porc(-4)',
'humedad_min_media_porc(-5)',
'humedad_min_media_porc(-6)',
'humedad_min_media_porc(-7)',
'humedad_min_media_porc(-8)',
'humedad_min_media_porc(-9)',
'humedad_min_media_porc(-10)',
'humedad_min_media_porc(-11)']]
df_reduced.dtypes
df_reduced.head()
df_reduced.describe()
max_values = df_reduced.max()
min_values = df_reduced.min()
# Normalización del dataset
df_normalizado = (df_reduced - df_reduced.min())/(df_reduced.max() - df_reduced.min())
df_normalizado.head()
Definición del conjunto de entrenamiento y de prueba¶
Y = df_normalizado[['cantidad']].to_numpy()
X = df_normalizado.drop(['cantidad'], axis=1).to_numpy()
Y[0], X[0]
len(X[0])
bunch_size = int(len(Y)/4)
bunch_size
x_train = X[0:len(Y)-bunch_size]
x_test = X[-bunch_size:]
y_train = Y[0:len(Y)-bunch_size]
y_test = Y[-bunch_size:]
len(y_train), len(y_test)
Definicion y Entrenamiento del Modelo¶
A modo de prueba se entrena y evalua un modelo centralizado
np.random.seed(0)
data = Tensor(x_train, autograd=True)
target = Tensor(y_train, autograd=True)
# model = Sequential([Linear(25,4), Relu(), Linear(4,3), Relu(), Linear(3,1), Sigmoid()])
# model = Sequential([Linear(25,4), Sigmoid(), Linear(4,5), Sigmoid(), Linear(5,1), Sigmoid()])
# model = Sequential([Linear(25,4), Relu(), Linear(4,6), Relu(), Linear(6,1), Sigmoid()])
# model = Sequential([Linear(25,4), Sigmoid(), Linear(4,6), Sigmoid(), Linear(6,1), Sigmoid()])
model = Sequential([Linear(25,4), Tanh(), Linear(4,6), Tanh(), Linear(6,1), Sigmoid()])
criterion = MSELoss()
# optim = SGD(parameters=model.get_parameters(), alpha=0.01)
optim = SGD(parameters=model.get_parameters(), alpha=0.01)
# 500
for i in range(500):
# Predecir
pred = model.forward(data)
# Comparar
loss = criterion.forward(pred, target)
# Aprender
loss.backward(Tensor(np.ones_like(loss.data)))
optim.step()
if (i%100 == 0):
print(loss)
test_data = Tensor(x_test)
test_target = Tensor(y_test)
pred = model.forward(test_data)
pred_list = [x[0] for x in pred.data]
test_target_list = [x[0] for x in test_target.data]
comparison = pd.DataFrame({'actual':test_target_list, 'predicted':pred_list})
comparison.head()
denormalized_pred_list = [(x[0] * (max_values['cantidad'] - min_values['cantidad'])) + min_values['cantidad'] for x in pred.data]
denormalized_test_target_list = [(x[0] * (max_values['cantidad'] - min_values['cantidad'])) + min_values['cantidad'] for x in test_target.data]
denormalized_comparison = pd.DataFrame({'actual':denormalized_test_target_list, 'predicted':denormalized_pred_list})
denormalized_comparison.head()
print('RMSE:',rmse(pred_list, test_target_list))
Modelo de Aprendizaje Federado con Cifrado Homomorfico¶
Como se dijo al inicio, vamos hacer las siguientes suposiciones sobre nuestro dataset:
- Se encuentra distribuido entre 3 instituciones
- Contienen datos confidenciales que no pueden ser compartidos entre sí ni a un tercero
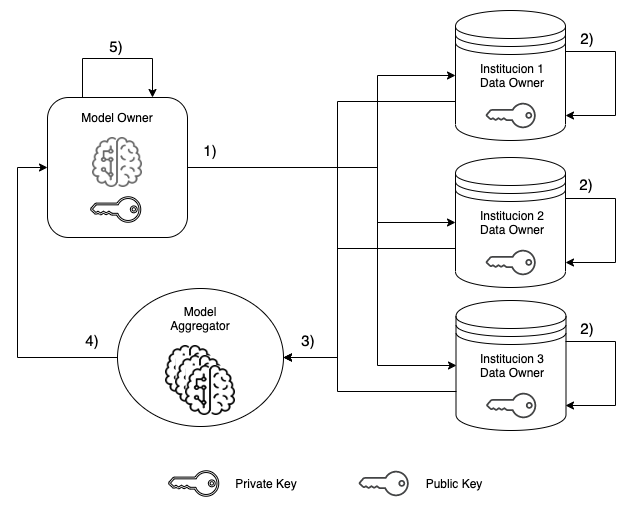
Con estas condiciónes, el siguiente codigo pretende mostrar como podemos obtener un modelo capaz de predecir casos de dengue sin la necesidad de que el dueño del modelo o (model owner) tenga que acceder directamente a los datos de las instituciones (data owners)
Definición de la arquitectura y del metodo de entrenamiento del modelo¶
np.random.seed(0)
data = Tensor(x_train, autograd=True)
target = Tensor(y_train, autograd=True)
layers = [Linear(25,4), Relu(), Linear(4,3), Relu(), Linear(3,1), Sigmoid()]
model = Sequential(layers)
def train(model, data, target, iterations=5, alpha=0.01, print_loss=True):
criterion = MSELoss()
optim = SGD(parameters=model.get_parameters(), alpha=alpha)
for i in range(iterations):
# Predecir
pred = model.forward(data)
# Comparar
loss = criterion.forward(pred, target)
# Aprender
loss.backward(Tensor(np.ones_like(loss.data)))
optim.step()
if (i%100 == 0 and print_loss):
sys.stdout.write("\r\tLoss:" + str(loss))
return model
Definicion de funciones auxiliares para manipular modelos encryptados¶
def encrypt_tensor(matrix, pubkey):
encrypt_weights = list()
for vector in matrix:
# print(vector)
for val in vector:
# print(val)
encrypt_weights.append(pubkey.encrypt(val))
restore = np.array(encrypt_weights).reshape(matrix.shape)
# print(restore)
return restore
def decrypt_tensor(matrix, privkey):
decrypted_weights = list()
for vector in matrix:
# print(vector)
for val in vector.flatten():
# print(val)
decrypted_weights.append(privkey.decrypt(val))
restore = np.array(decrypted_weights).reshape(matrix.shape)
# print(restore)
return restore
def encrypt_sequential_model(model, pubkey):
for layer in model.layers:
if type(layer) == Linear:
layer.weight.data = encrypt_tensor(layer.weight.data, pubkey)
return model
def decrypt_sequential_model(model, n_models, privkey):
for layer in model.layers:
if type(layer) == Linear:
layer.weight.data = decrypt_tensor(layer.weight.data, privkey)/n_models
return model
def zero_sequential_model(model):
for layer in model.layers:
if type(layer) == Linear:
layer.weight.data = np.zeros_like(layer.weight.data)
return model
def aggregate_models(list_of_models):
aggregated_model = zero_sequential_model(copy.deepcopy(list_of_models[0]))
# print(list_of_models)
for model in list_of_models:
# print(model)
for i in range(len(model.layers)):
if type(model.layers[i]) == Linear:
aggregated_model.layers[i].weight.data += model.layers[i].weight.data
return aggregated_model
def train_and_encrypt(model, data, target, pubkey, iterations=50, alpha=0.01, print_loss=True):
new_model = train(copy.deepcopy(model), data, target, iterations, print_loss=print_loss)
encrypted_model = encrypt_sequential_model(new_model, pubkey)
return encrypted_model
Prueba de la funcion de entrenamiento¶
new = train(model, data, target, iterations=500)
Pruebas de creación de un modelo encriptado¶
public_key, private_key = phe.generate_paillier_keypair(n_length=128)
np.random.seed(0)
data = Tensor(x_train, autograd=True)
target = Tensor(y_train, autograd=True)
layers = [Linear(25,4), Relu(), Linear(4,3), Relu(), Linear(3,1), Sigmoid()]
model = Sequential(layers)
for i in range(9):
model = train_and_encrypt(model, data, target, public_key)
model = aggregate_models([model])
model = decrypt_sequential_model(model, 1, private_key)
pred = model.forward(test_data)
pred_list = [x[0] for x in pred.data]
test_target_list = [x[0] for x in test_target.data]
print('RMSE:',rmse(pred_list, test_target_list))
Distrubución del dataset en las diferentes Instituciones¶
Inicializamos las entidades distribuyendo el dataset entre las tres y definimos un perceptron multicapa para realizar una regresión (predecir el numero de casos futuros)
np.random.seed(0)
rangos = list()
for i in range(4):
rangos.append(int((len(x_train)/3)*i))
# print(rangos)
data_entidad_01 = Tensor(x_train[rangos[0]:rangos[1]], autograd=True)
target_entidad_01 = Tensor(y_train[rangos[0]:rangos[1]], autograd=True)
data_entidad_02 = Tensor(x_train[rangos[1]:rangos[2]], autograd=True)
target_entidad_02 = Tensor(y_train[rangos[1]:rangos[2]], autograd=True)
data_entidad_03 = Tensor(x_train[rangos[2]:rangos[3]], autograd=True)
target_entidad_03 = Tensor(y_train[rangos[2]:rangos[3]], autograd=True)
layers = [Linear(25,4), Relu(), Linear(4,3), Relu(), Linear(3,1), Sigmoid()]
model = Sequential(layers)
# print(len(data_entidad_01.data))
# print(len(data_entidad_02.data))
# print(len(data_entidad_03.data))
np.random.seed(0)
layers = [Linear(25,4), Relu(), Linear(4,3), Relu(), Linear(3,1), Sigmoid()]
# layers = [Linear(25,4), Relu(), Linear(4,4), Relu(), Linear(4,1), Sigmoid()]
# layers = [Linear(25,4), Relu(), Linear(4,5), Relu(), Linear(5,1), Sigmoid()]
# layers = [Linear(25,4), Tanh(), Linear(4,3), Tanh(), Linear(3,1), Sigmoid()]
# layers = [Linear(25,4), Relu(), Linear(4,1), Sigmoid()]
# model = Sequential([Linear(25,4), Tanh(), Linear(4,6), Tanh(), Linear(6,1), Sigmoid()])
model = Sequential(layers)
for i in range(9):
print('\nIniciando la ronda de entrenamiento Nro:', i+1)
print('\tPaso 1: enviamos el modelo a Institucion 01')
entidad_01_encrypted_model = train_and_encrypt(model,
data_entidad_01,
target_entidad_01,
public_key, iterations=50, alpha=0.007)
print('\n\tPaso 2: enviamos el modelo a Institucion 02')
entidad_02_encrypted_model = train_and_encrypt(model,
data_entidad_02,
target_entidad_02,
public_key, iterations=50, alpha=0.007)
print('\n\tPaso 3: enviamos el modelo a Institucion 03')
entidad_03_encrypted_model = train_and_encrypt(model,
data_entidad_03,
target_entidad_03,
public_key, iterations=50, alpha=0.007)
print('\n\tPaso 4: Institucion 01, Institucion 02 y Institucion 03 envian')
print('\ty agregan sus modelos encriptados ente sí')
models_list = [entidad_01_encrypted_model,
entidad_02_encrypted_model,
entidad_03_encrypted_model]
encrypted_model = aggregate_models(models_list)
print('\n\tPaso 5: Solo el modelo agregado')
print('\tse envia devuelta al dueño del modelo')
print('\tque puede desencriptarlo')
model = decrypt_sequential_model(encrypted_model, len(models_list), private_key)
pred = model.forward(test_data)
pred_list = [x[0] for x in pred.data]
test_target_list = [x[0] for x in test_target.data]
print('RMSE:',rmse(pred_list, test_target_list))
comparison = pd.DataFrame({'actual':test_target_list, 'predicted':pred_list})
comparison.head()
Como se puede ver en los resultados, el modelo obtenido es casi tan bueno que el modelo entrenado de forma centralizada.
Notas Finales¶
Si bien los resultados no logran ser tan buenos como los resultados obtenidos en el paper, se logra demostrar que es posible entrenar un modelo con un performance relativamente bueno sin necesidad de acceder directamente a los datos. Con una mejora en la busqueda de los hiperparametros se podría mejorar aún más el performance del modelo.
Grid Search¶
Prueba para encontrar un mejor modelo usando Grid Search
np.random.seed(0)
alphas = [0.001,
0.003,
0.005,
0.007,
0.01,
0.01,
0.03,
0.05]
architectures = [[Linear(25,1), Sigmoid()],
[Linear(25,4), Sigmoid(), Linear(4,3), Sigmoid(), Linear(3,1), Sigmoid()],
[Linear(25,4), Tanh(), Linear(4,3), Tanh(), Linear(3,1), Sigmoid()],
[Linear(25,4), Relu(), Linear(4,3), Relu(), Linear(3,1), Sigmoid()],
[Linear(25,4), Sigmoid(), Linear(4,5), Sigmoid(), Linear(5,1), Sigmoid()],
[Linear(25,4), Tanh(), Linear(4,5), Tanh(), Linear(5,1), Sigmoid()],
[Linear(25,4), Relu(), Linear(4,5), Relu(), Linear(5,1), Sigmoid()],
[Linear(25,5), Sigmoid(), Linear(5,6), Sigmoid(), Linear(6,1), Sigmoid()],
[Linear(25,5), Tanh(), Linear(5,6), Tanh(), Linear(6,1), Sigmoid()],
[Linear(25,5), Relu(), Linear(5,6), Relu(), Linear(6,1), Sigmoid()]]
best_model = {}
actual_rmse = 100.0
for architecture in architectures:
for alpha in alphas:
model = Sequential(copy.deepcopy(architecture))
for i in range(10):
entidad_01_encrypted_model = train_and_encrypt(model,
data_entidad_01,
target_entidad_01,
public_key, iterations=50, alpha=alpha)
# print('\n\tPaso 2: enviamos el modelo a Institucion 02')
entidad_02_encrypted_model = train_and_encrypt(model,
data_entidad_02,
target_entidad_02,
public_key, iterations=25, alpha=alpha)
# print('\n\tPaso 3: enviamos el modelo a Institucion 03')
entidad_03_encrypted_model = train_and_encrypt(model,
data_entidad_03,
target_entidad_03,
public_key, iterations=25, alpha=alpha)
# print('\n\tPaso 4: Institucion 01, Institucion 02 y Institucion 03 envian')
# print('\ty agregan sus modelos encriptados ente sí')
models_list = [entidad_01_encrypted_model,
entidad_02_encrypted_model,
entidad_03_encrypted_model]
encrypted_model = aggregate_models(models_list)
# print('\n\tPaso 5: Solo el modelo agregado')
# print('\tse envia devuelta al dueño del modelo')
# print('\tque puede desencriptarlo')
model = decrypt_sequential_model(encrypted_model, len(models_list), private_key)
pred = model.forward(test_data)
pred_list = [x[0] for x in pred.data]
# test_target_list = [x[0] for x in test_target.data]
new_rmse = rmse(pred_list, test_target_list)
if (new_rmse < actual_rmse):
print('\tNuevo mejor RMSE:',new_rmse)
actual_rmse = new_rmse
best_model['model'] = model
best_model['architecture'] = architecture
best_model['alpha'] = alpha
best_model['rmse'] = actual_rmse
print(best_model['rmse'])
print(best_model['alpha'])
print(best_model['architecture'])
Apartado de pruebas de las funciones de Cifrado Homomorfico (Homomorphic Encryption)¶
Pruebas relizadas para las metodos de encriptado, agregación y desencriptado de un modelo
aux = Sequential([Linear(3,2)])
aux.layers[0].weight.data
encripted_tensor = encrypt_tensor(aux.layers[0].weight.data, pubkey=public_key)
decrypt_tensor(encripted_tensor, privkey=private_key)
seq_aux = Sequential([Linear(2,3), Linear(3,2)])
print(seq_aux.layers[0].weight.data)
print()
encrypted_model = encrypt_sequential_model(seq_aux, pubkey=public_key)
print(encrypted_model.layers[0].weight.data)
print()
decrypted_model = decrypt_sequential_model(encrypted_model, n_models=1, privkey=private_key)
print(decrypted_model.layers[0].weight.data)
zero_seq = zero_sequential_model(seq_aux)
print(zero_seq.layers[1].weight)
new_model = aggregate_models([aux, aux])
print(aux.layers[0].weight.data)
print(new_model.layers[0].weight.data)