En lugar de calcular manualmente el gradiente de cada capa obteniendo la derivada del resultado de la capa anterior, los frameworks de deeplearning hacen esto de forma automática. Para poder agregar esta funcionalidad, debemos agregar a los tensores la capacidad de crear algo llamado Grafo computacional

Grafo Computacional o computational grapg

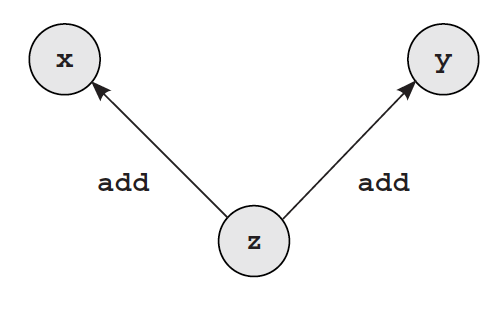
Para poder realizar retropropagación o backprop sobre una red neuronal, debemos ser capaces de poder rastrear y determinar todas las operaciones y transformaciones que son realizadas sobre los tensores que componen la arquitectura de la red. Para esto definimos lo que se llama un grafo computacional. Que básicamente, si obtuvimos un tensor z a partir de la suma de los tensores x e y, luego de obtener el valor de z y el error, debemos poder propagar el error por el resto de los tensores que participaron en la creacion de z es decir por x e y y teniendo en cuenta la operación mediante la cual se combinaron.

Para esto debemos agregar a la clase Tensor los siguientes atributos:

• creators: que es una lista de tensores que originaron el nuevo tensor y
• creation_op: que permite saber qué operacion utilizaron los creators para combinarse y crear el nuevo tensor

import numpy as np

class Tensor(object):
    
    def __init__(self, data, creators=None, creation_op=None):
        '''
        Inicializa un tensor utilizando numpy
        
        @data: una lista de numeros
        @creators: lista de tensores que participarion en la creacion de un nuevo tensor
        @creators_op: la operacion utilizada para combinar los tensores en el nuevo tensor
        '''
        self.data = np.array(data)
        self.creation_op = creation_op
        self.creators = creators
        self.grad = None
        
    def backward(self, grad):
        '''
        Funcion que propaga recursivamente el gradiente a los creators del tensor
        
        @grad: gradiente 
        '''
        self.grad = grad
        
        if (self.creation_op == 'add'):
            self.creators[0].backward(grad)
            self.creators[1].backward(grad)
        
    def __add__(self, other):
        '''
        @other: un Tensor
        '''
        return Tensor(self.data + other.data,
                      creators=[self, other],
                      creation_op='add')
    
    def __repr__(self):
        return str(self.data.__repr__())
    
    def __str__(self):
        return str(self.data.__str__())

one = Tensor([1,1,1,1,1])
x = Tensor([1,2,3,4,5])
y = Tensor([2,2,2,2,2])
z = x + y
z.backward(one)

print('gradientes')
print('z', z.grad)
print('x', x.grad)
print('y', y.grad)

gradientes
z [1 1 1 1 1]
x [1 1 1 1 1]
y [1 1 1 1 1]

Como el gradiente de una suma es la suma, podemos ver que los gradientes para los creators es el valor al cual hicimoz backward, en este caso [1,1,1,1,1]

Como backward propaga el gradiente de forma recursiva, veamos que ocurre si creamos un grafo computacional más profundo

a = Tensor([2,2,2,2])
b = Tensor([3,3,3,3])
c = Tensor([4,4,4,4])
d = a + b
e = c + d
e.backward([1,1,1,1])
print(a.grad)

[1, 1, 1, 1]

a = Tensor([1,2,3,4,5])
b = Tensor([2,2,2,2,2])
c = Tensor([5,4,3,2,1])
d = a + b
e = b + c
f = d + e
f.backward(Tensor([1,1,1,1,1]))
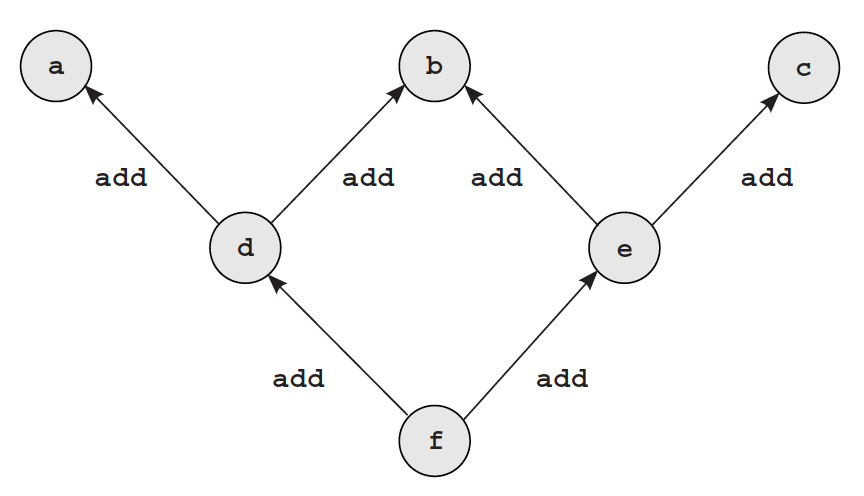
print(b.grad.data == np.array([2,2,2,2,2]))

[False False False False False]

El gradiente [1,1,1,1,1] es pasado a b dos veces, por lo que dicho gradiente se debería sumar y ser [2,2,2,2,2] pero en lugar de eso sigue siendo [1,1,1,1,1]. En el siguiente notebook se agregará soporte a la clase Tensor para solucionar este problema